작성일 In 댓글:

Project Euler

  • 공식 홈페이지 - projecteuler.net
  • 한글 번역 - projecteuler @kr
  • (HackerRank) ProjectEuler+ - hackerrank.com

Problem

Sum square difference


problem <번역>

solution

Simple Code

컴퓨터는 연산이 빠르기 때문에 Brute Force한 방법으로 그냥 단순히 반복문을 통해 다 더하여 답을 구할 수도 있다.

006_sum_square_difference.py
def sum_of_num(n):
  total = 0
  for i in range(1, n+1):
      total += i

  return total**2


def sum_of_square_num(n):
  total = 0
  for i in range(1, n+1):
      total += i**2

  return total


print(sum_of_num(100) - sum_of_square_num(100))
HackerRank

하지만 조금이라도 효율적인 성능을 이끌어 내기 위해서는 수식을 이용한 풀이가 더 적당할 것 같다.
n까지의 단순 합은 n(n+1)/2와 같고
n까지의 제곱 합은 (2n+1)(n+1)n/6과 같다.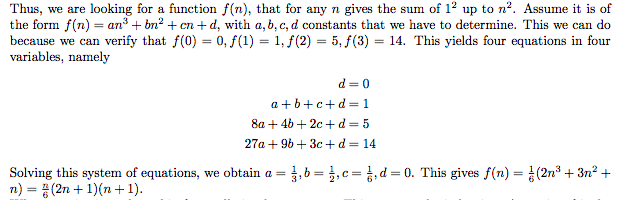

006_for_HacerRank.py
def sum_of_num(n):
  total = n*(n + 1)//2
  return total**2


def sum_of_square_num(n):
  return (2*n + 1)*(n + 1)*n//6


if __name__ == '__main__':
  for _ in range(int(input())):
      num = int(input())
      print(sum_of_num(num) - sum_of_square_num(num))

제곱의 합 공식

작성일 In 댓글:

Project Euler

  • 공식 홈페이지 - projecteuler.net
  • 한글 번역 - projecteuler @kr
  • (HackerRank) ProjectEuler+ - hackerrank.com

Problem

Smallest multiple


problem <번역>

solution

Simple Code

최소 공배수를 찾는 문제이다.
최대 공약수, 최소 공배수를 찾을 때 유클리드 호제법을 응용한 유클리드 알고리즘을 사용하면 쉽다.

005_smallest_multiple.py
def gcd(a, b):
  while b > 0:
      a, b = b, a % b

  return a


def lcd(a, b):
  return a * b // gcd(a, b)


def smallest_multiple(n):
  cur = 1

  for num in range(1, n+1):
      cur = lcd(cur, num)

  return cur


print(smallest_multiple(20))
HackerRank

테스트 케이스 입력 받는 부분만 추가해 주면 된다.

005_for_HacerRank.py
def gcd(a, b):
  while b > 0:
      a, b = b, a % b

  return a


def lcd(a, b):
  return a * b // gcd(a, b)


def smallest_multiple(n):
  cur = 1

  for num in range(1, n+1):
      cur = lcd(cur, num)

  return cur


if __name__ == '__main__':
  for _ in range(int(input())):
      print(smallest_multiple(int(input())))

유클리드 호제법을 잘 이해하고 있다면 쉽게 풀 수 있는 문제이다.

작성일 In 댓글:

Project Euler

  • 공식 홈페이지 - projecteuler.net
  • 한글 번역 - projecteuler @kr
  • (HackerRank) ProjectEuler+ - hackerrank.com

Problem

Largest palindrome product


problem <번역>

solution

Simple Code

세자리 수 중 가장 큰 999부터 하나씩 곱해가며 가장 큰 수를 구한다.
큰 숫자 중 문자열 비교를 통해 숫자가 대칭인지 확인한다.

004_largest_palindrome_product.py
def largest_palindrome_product():
  largest = 0
  for i in range(999, 100, -1):
      for j in range(i, 100, -1):
          product = i * j
          if product > largest:
              s_product = str(product)
              if s_product == s_product[::-1]:
                  largest = product

  return largest


print(largest_palindrome_product())
HackerRank

HackerRank 문제에서는 정수 N을 입력 받아 해당 정수보다 작은 palindrome number를 출력해야 한다.
그래서 리스트에 저장하고 역순으로 정렬하여 반복문을 통해 조건을 확인하는 방식으로 작성했다.

004_for_HacerRank.py
def largest_palindrome_product():
  palindrome = []

  for i in range(999, 100, -1):
      for j in range(i, 100, -1):
          product = i * j
          if product not in palindrome:
              s_product = str(product)
              if s_product == s_product[::-1]:
                  palindrome.append(product)

  return sorted(palindrome, reverse=True)


if __name__ == '__main__':
  palindromeList = largest_palindrome_product()

  for _ in range(int(input())):
      N = int(input())
      for p in palindromeList:
          if p < N:
              print(p)
              break

palindrome number의 자리수가 짝수일 때, 11로 나누어 떨어진다.
예를 들어 a, b, c가 정수이고 a != 0 일 때,
N(6, a, b, c) = 100001 * a + 10010 * b + 1100 * c
= abccba = 11 * (9091 * a + 910 * b + 100 * c)
N(8, a, b, c,d) = 10000001 * a + 1000010 * b + 100100 * c + 11000 * d
= abcddcba = 11 * (909091 * a + 90910 * b + 9100 * c + 1000 * d)
임을 확인할 수 있다.

주의할 것은 해당 문제에서 세자리 수 2개를 곱한 값의 자리수가 꼭 짝수는 아니다.
예를 들어,
777 * 117 = 90909 (5자리)
812 * 104 = 84448 (5자리)
813 * 123 = 99999 (5자리)
이러한 palindrome number는 11로 나누어지지 않는다.

어쨌든 최대값을 구하는 것이기 때문에 위 내용을 활용해서 조금 더 최적화 시킬 수 있는데 아래의 링크에서 자세히 설명되어 있다.
Project Euler 4 Solution: Largest palindrome product